Overview#
The goal of this package is to estimate the stellar background. In this context, “stellar background” means any time-steady signal at each fixed celestial coordinate (i.e. each right ascension–declination coordinate). This includes both stars and diffuse sources such as the Milky Way, but excludes planets and any other “foreground” sources, such as the extended solar corona. Additionally, stellar variability is ignored. This estimating process produces an all-sky map (or rather, a map of that portion of the sky that your input images cover) of this estimated background. Once this background map has been produced and processed, it can be subtracted out of each of the input images (or any other similar images).
The intended application of this package is for solar/heliospheric image sets, in which the stellar background is a contaminant amidst the foreground signal of the solar corona.
Note that this package includes a Jupyter notebook demonstrating the use of this package with WISPR data.
Input data#
It is assumed that your input data set is a collection of celestial images in which large-scale foreground sources (such as the extended solar corona) have been largely suppressed. These images must have celestial WCS information that is sub-pixel accurate, and the point-spread function (PSF) must be uniform across the image plane and from image to image. The flux calibration of the images must be consistent, so that stars don’t vary in time (except for any intrinsic variability).
Preparing the input data#
In many cases, it will be important to pre-process the input data. This can include steps such as regularizing the PSF. (The regularizepsf package may be useful for this.) Another important factor at this stage is ensuring that all the input images have the same average background level (that is, the pixel value where there is no other signal). If your images tend to have a constant offset from zero and that offset varies through your image sequence, then in the next step where the images are stacked and reduced, the selected value will be biased by the varying background. This type of time-varying background should be leveled in this pre-processing stage. Additionally, if you have a constant background offset, that offset will become part of the starfield estimate, and it will therefore be subtracted from your images along with the starfield. You may therefore desire to zero out the offset for the images that go into the starfield estimation.
The latter stages will benefit if the input images are as clean as possible. Planets and any other transients (for WISPR, this includes the frequent debris streaks) should be masked. (Replacing them with NaNs will have those pixels ignored in later steps.) Any coronal signals, from both the K and F corona, should be removed to the extent possible. (With WISPR, I use L3 images where the F-corona has been estimated and removed, and I subtract from each pixel the value predicted by a bilinear function fit to the pixel values in a small region around the pixel—effectively linearizing and subtracting the K corona from most regions.)
Implementation Note#
If the total amount of pre-processing is small, it can be done “live” as the
images are loaded for the estimation step. This is done by implementing the
preprocessing logic in a subclass of ImageProcessor. If the total
preprocessing is large, then it may be advantageous to save out pre-processed
images and use those for starfield estimation. This both speeds up iteration as
you adjust estimation parameters, and speeds up estimation, since each image is
loaded multiple times. Some pre-processing steps, such as PSF regularization,
must also be done to the images from which the starfield will be subtracted, to
ensure stellar shapes and fluxes match up. For these steps, it may therefore be
very useful to encode the logic in your ImageProcessor subclass.
Estimating the starfield#
The starfield estimate is generated, in short, by reprojecting all the images into a common all-sky celestial frame, and then reducing the collection of values at each pixel (i.e. each celestial coordinate) in that frame.
Several reduction functions are provided in this package, and the user can
easily implement their own by subclassing StackReducer.
Implementation Note#
The simplest approach to this “reproject, stack, and reduce” workflow would be
to reproject all images into arrays the size of the all-sky map (which will
be mostly empty pixels outside the image bounds, meaning the memory use will be
much larger than just loading the images themselves into memory), and then
reducing to build the final map. The memory usage of this approach is
prohibitive for all but the smallest sets of input images. Instead, the output
map is divided into several vertical strips. For each strip, this package
reprojects all images into arrays the size of the strip, avoiding any
reprojection work or memory use for images which don’t span the strip, and then
reduces to form the output for that strip. This produces large memory savings,
but all work that occurs in ImageProcessor is repeated for each image that
spans multiple strips. You may therefore want to keep your ImageProcessor
subclass light, or implement a caching strategy if you must do more substantive
processing and have the memory to spare.
The size of the vertical strips is by the target_mem_usage argument to
build_starfield_estimate. The size of strips is set so that, considering the
total number of input images and the size of the all-sky map, the maximum size
of the strip’s accumulation array can’t exceed this amount. If each strip has
some images which don’t span the strip, the whole accumulation array won’t be
used. And since the accumulation array is allocated with np.empty, the full
amount of memory may never be used, as, depending on your operating system, the
memory won’t be reserved and allocated until it is actually accessed. It may
therefore be reasonable to set target_mem_usage higher than your actual
amount of memory so that the portion actually used is closer to the amount of
free memory you have available.
Reduction Methods#
Gaussian Reduction#
At each output-map pixel coordinate, outliers are iteratively removed from the set of samples based on a “n standard deviations” criterion. Then the collection of samples is converted into a histogram, and that histogram is fit with a Gaussian function, whose center is taken as the estimated background value. A sqrt(N) weighting has the fit focus mostly on the bins with many samples. This scheme is ideal of the collection of samples is mostly a noisy distribution around a single “true” background value.
Note that despite performing individual fits for each pixel in the output map, this reduction method isn’t unduly slow.
This method is implemented, with variations, by GaussianReducer,
GaussianAmplitudeReducer, and MeanReducer.
Skew-Gaussian Reduction#
This method is very similar to Gaussian reduction, but the fitted function is a skewed Gaussian, potentially allowing the function to better fit distributions that resemble a Gaussian-noise distribution of “clean” samples, plus a tail of brighter samples when foreground signals are present.
This method is implemented by SkewGaussianReducer.
Percentile Reduction#
At each output-map pixel coordinate, a low percentile value is selected as the output value. That value is taken as the “cleanest” sample of the fixed celestial background at that coordinate—that is, the sample most free of any foreground signal. (Using a low percentile rather than the minimum reduces the impact of outlier values, artifacts, and any other oddities.) This may be the ideal reduction method if many or most samples at each coordinate contain additional contamination and there are few “clean” samples. This method can be prone to underestimation, as the low percentile can easily fall on the low-side tail of the distribution of “clean” samples. This underestimation can be prone to varying based on the brightness of the pixel in question, as the same distribution of contaminant signals will be less significant on top of a very bright background, leaving a larger number of “clean” samples and causing the low percentile to therefore be further from the center of the “clean sample” distribution. Some success can be had in fitting a correction factor as a function of pixel brightness that minimizes the similarity between pixels in an image to be subtracted and the starfield estimate for that image.
This method is implemented by PercentileReducer.
Results#
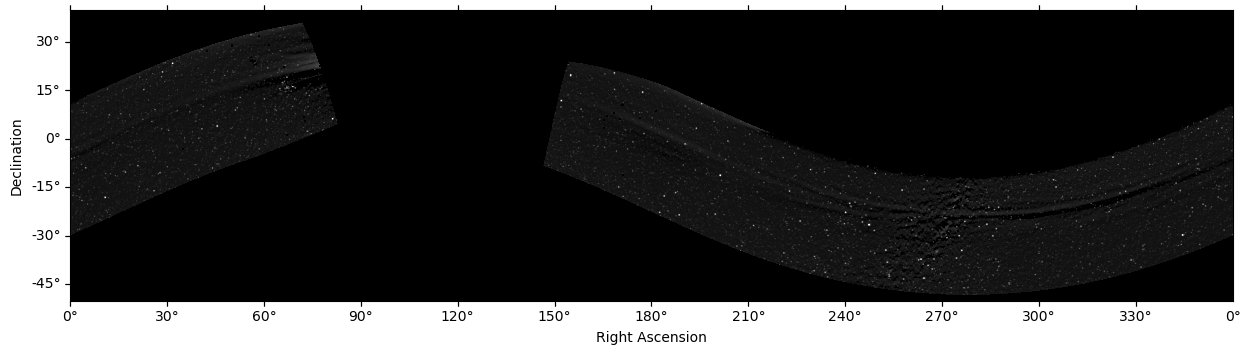
This all-sky map shows the estimated stellar background from a large number of PSP/WISPR images. As PSP sweeps through each of its encounters, the WISPR camera rapidly pans across the sky (with its pointing always fixed relative to the spacecraft orientation, which is itself locked to the Sun’s direction to ensure heatshield alignment). This produces the sinusoidal pattern (reflecting the misalignment between PSP’s orbital plane and the Earth axis—and therefore the RA/Dec equator) and a gap (reflecting the portion of each PSP orbit in which WISPR is not imaging). The Milky Way can be seen clearly.
Two main artifacts are present:
At the left-hand edge of the gap, significant coronal signals can be seen, as those coordinates are only ever imaged very close to the Sun, right before each WISPR image sequence ends.
Stretching through the entire sequence about a third of the way down from the top of the imaged region is a band of dark and light streaks. This is along the PSP orbital plane which is Venus’s orbital plane and is close to the solar equatorial plane. This ensures a persistent presence of foreground signals, such as the Venus orbital dust ring and the heliospheric plasma sheet, which in turn leave artifacts in the background estimate.
Subtracting images#
To remove the stars from an individual image, the starfield estimate is
reprojected into the frame of the target image and subtracted out. The input
image must be adequately prepared first. Some of the pre-processing steps that
were applied to the input images when generating the starfield estimate must
also be applied to the input image in the subtraction stage. This includes
steps such as PSF correction, to ensure that the shapes of stars in the input
image are the same as their shapes in the starfield estimate. The reprojection
used (“adaptive resampling”) ensures proper antialiasing, which inherently
produces a slight Gaussian blur in the output image, on the order of a couple
pixels. As the starfield data has been reprojected twice (once into the all-sky
frame and once back into the target image’s frame), the input data should also
receive two passes of the same Gaussian blurring, to again ensure that the
shapes of stars line up correctly. This blurring is automatically provided by
Starfield.subtract_from_image.

An example of an input image (from PSP/WISPR), the corresponding estimated starfield, and the result of the subtraction. A few black regions in the images mark detector defects, and the large bright “star” in the upper right is a planet. Slightly bipolar spots (dark and bright regions side-by-side) in the upper-left corner of the subtracted image indicate slight misalignments between the starfield estimate and the actual star (likely small inaccuracies in the lens distortion information in that corner).#
Checking starfield quality#
There are two main ways to evaluate the quality of the starfield estimate. The first is by visually inspecting starfield-subtracted images. This will immediately reveal significant over- or under-subtractions (i.e. bad estimates of the star’s brightness in the starfield). It will also quickly reveal and issues with the pointing/coordinate information in your data, as any misalignments will produce bipoles of over- and under-subtraction, and time-variation of the alignment will produce “leftover” flux at the location of bright stars that can be seen to wobble and flicker in a video of subtracted images.
The other main way is by applying aperture photometry at the locations of known stars and inspecting
catalog magnitude values versus the (log of the) measured fluxes in the starfield estimate.
stellar fluxes in the starfield estimate versus those in the input images
remnant flux in a star’s location after subtraction, visualized as a function of expected flux values or magnitudes
remnant flux as a fraction of initial flux, again visualized as a function of expected flux values or magnitudes